Profile of MMX

Thanks for the math. Somehow it makes very clear why the 76mm overall isn't worth it. If you look at it, you'll see that you need 51 seconds for a 50% chance at 40 meters to kill a Panther with the shell that is meant to kill tanks and does next to no damage vs infantry. Meanwhile Panther needs 20 seconds to 100% destroy a 76mm Sherman at 50 meters. Even factoring in population values doesn't change the outcome (you get 1,5 76mm Shermans for 1 Panther). It just closes the gap a little bit, but it is still far apart.

true, a 76mm sherman won't scare off a panther, whether with or without hvap munitions. however, it would arguably be kind of nuts if it were an actual threat to it as both tanks serve fundamentally different roles, have different costs/timings and also differ in their ai potential. i see the 76 mm more as a hybrid between the regular sherman and the jackson, though you can probably argue it's not too effective in either at or ai compared to the two. since the last patches first and foremost gutted its anti-inf performance, i'd agree that a small ai buff to the regular at rounds might be a good call. still, i think the hvap is fine for what it does and shouldn't be made any more powerful.

Thanks for this, I was hoping someone with more knowledge on probability would come along and do real math instead of my boot legged version of probability.

It depicts a different picture in regards to HVAP vs AP but I think one important element missing is there are more 'rolls' on AP than there are on HVAP. Namely that AP will shoots faster which means with every shot, there is a chance for a Panther to die.

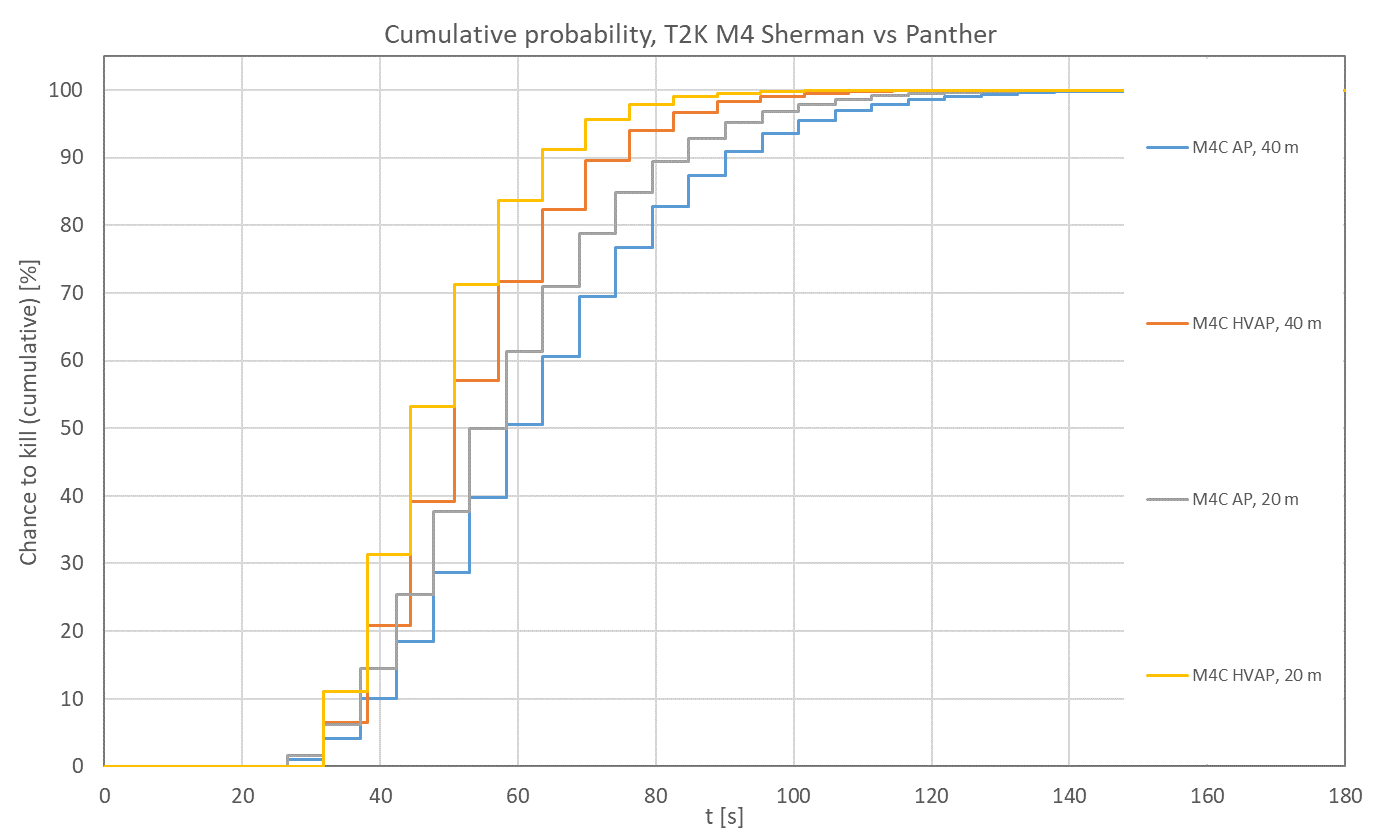
Taking the second chart into account, cumulative probability T2K. If we stop at the 60s mark, AP will have had 6 rolls/chances to kill with each shot while HVAP only has 5. I don't think accuracy can make up that lost chance/gap right? I suppose we can add up all the chances here and average them out and see which one is higher?

Picture:



I think I mentioned in the first post but its hard to calculate the accuracy since the first shot would likely be a moving shot as well. Assuming all shots hit, HVAP doesn't seem much better. Especially with the 6s switch time.

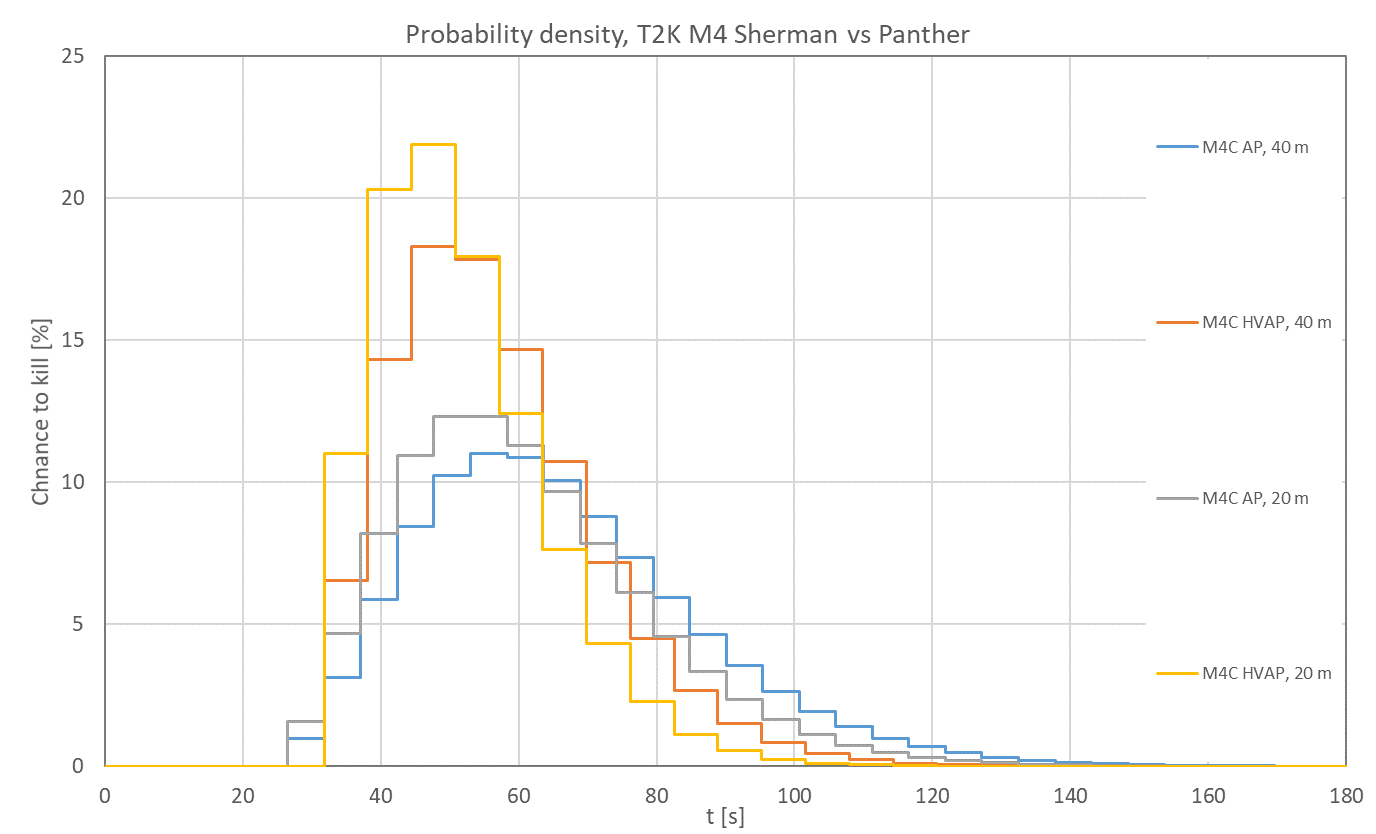
I guess it would be a good idea to clarify the 2nd graph a bit more and what these probabilities imply. Basically there are two ways to read the info in there.

1) If you look at a certain timestamp, e.g. the 60 second mark as in your example, the y-value of the curves will tell you the probability the M4C will have killed the Panther (i.e. out of all shots fired 6 penetrating hits have been scored) within 60 s or less. In this case, the AP Sherman at 40 m (blue line) will have a kill probability of a bit over 50%, while the HVAP Sherman (red line) will have killed the Panther in over 70% of all cases. Hence, the HVAP Sherman is more likely to knock out its target within 60 s.

2) If you pick a certain percentage on the y-axis, the respective value on the x-axis will tell you the average time it takes to kill the Panther with that confidence. If we, for example, pick a success probability of 50% the AP Sherman will need at least ~58 s to kill the Panther in 50 out of 100 cases, while the HVAP Sherman only needs around 51 s to do the same. If you increase the confidence level even more to 75% (i.e. out of 100 tries, the Panther is killed at least 75 times) the gap between the time it takes both tanks on average to knock out the target in at least 3/4 of all cases increases even more.

Note that these graphs already factor in ROF, not only penetration, so the extra round fired by the AP Sherman after ~7 firing cycles is already part of the equation (the horizontal gaps between the jumps in the graph are slightly shorter for the AP Sherman).

Ideally, the difference in accuracy should of course also be considered. But since this is (with my limited understanding of math at least) hard to implement into the probability calculation I used we'll have to treat this as an additional layer of RNG on top. And that's not even considering scatter shots which are even harder to compute deterministically.
However, the HVAP Sherman is vastly superior at all ranges here, so it should perform even better comparatively in an in-game head-to-head matchup than these graphs suggest.

If I'm understanding you correctly, you area saying that there is aim time that makes RoF slightly longer? I'm not sure what you're trying to say.

75mm Sherman (according to my CoH2 tools page) has a min reload of 5.6 and max reload of 6 so I don't know where you got that 6.05 from unless you are adding aim time.

You are right that the first shot shouldn't be counted though but if we subtract times from the averages, it doesn't change much.

Unbuffed max range (40). AP reload average at 5.05s.
HVAP TTK = 54.9s - 6.1s = 48.8s
AP TTK = 50.5s - 5.05s = 45.45s

At mid range (20).
HVAP TTK = 48.8s - 6.1s = 42.7s
AP TTK = 45.5s - 5.05s = 40.45s

I welcome you to redo the match I had on the initial post with your changed numbers. I doubt that would show a significant change on HVAP being better against heavy armour, which is its intended role, than AP in the long run. In short engagements where you are not expected to kill or chase, slightly better perhaps, in the long term it is not.

There's also the first shot accuracy due to moving into position which isn't calculated in but again, I'm doing the averages for in a light box to prove that HVAP is not better than AP for heavy armour.

I don't think the aim time makes much of a difference here since it's only one frame (0.125 s). More importantly, there are also no further hidden delays, such as wind up / wind down so your average numbers (minus the 1st shot) are pretty accurate.

However, I wouldn't be so quick to discount the accuracy difference between the two shells as negligible. The HVAP round has a 40% (!) higher chance to hit at max range, which is huge especially when moving / chasing. This alone makes it very much worthwhile even though the penetration-corrected DPS is even slightly in favor of the normal AP round.



EDIT: Looking over your numbers I think there's a glitch in your math; specifically, this part:

[...]It takes 6 shots to kill a Panther with 160 damage so on average, it will take a minimum of 6.1 * 6 = 36.6s to kill a Panther assuming all shots hit. The Panther will bounce some shots though, 36.5% chance to bounce. So that means our 6 shots to kill averages to 9 shots to kill a Panther at long range (6 * 1.365 = 8.19 or rounded up to 9). 9 shots to kill would mean 6.1 * 9 = 54.9s to kill a Panther in a light box. The Panther is expected to bounce 2-3 shots.

You multiply the minimum number of shots by (1 + chance to bounce), which isn't quite how this works. You can easily see this if you look at the extreme situation where you'd have a 100% chance to bounce. With your formula, the average number of shots to kill would go up by a factor of 2 only, while actually it should go to infinity (since there's no deflection damage involved).

If you instead divide the minimum number of shots by the chance to penetrate you'll get a more accurate value (e.g. 6 shots with 50% pen gives 6/0.5 = 12).

Difference being that max range the LeFH has a chance in hell of actually hitting anything intentionally. and when one person builds howitzers in their base to pressure the VPs, the other person has to more aggressively* place them (read: more vulnerably) to get them within range. So in a howitzer dual, the LeFH still has a distinct advantage, even without its busted counter barrage ability

all good and well, but how is that different from an allied player building an ml-20 to shell the vp area from the safety of their base and the axis player being hard-pressed to counter it?

also, both ml-20 and lefh are virtually carbon copies of each other, so i don't quite see why the lefh should have the advantage in an arty duel.

Are you sure thats how bare bones the calculation is ? 4% sounds like at gun vs infantry odds lol.

From personal experience, a tanks accuracy makes a literal night and day difference in infantry effectiveness when moving vs stationary and im aware its a 50% hit but +10% is definitely not negligible and do you know if the comet still has .75% moving accuracy ?

His calculation is 100% accurate. Tank gun accuracy has virtually no effect vs infantry and the AT-gun odds analogy is hitting the nail on the head. 10% more to a 4-5% chance to hit is still abysmally small. Hence, the moving accuracy debuff also doesn't make much of a difference unless you aim at something considerably bigger than an infantry model.

IIRC, the Comet's moving acc should be 0.5 as for most british tanks